La matemática es una de las únicas áreas del conocimiento que puede ser objetivamente descrita como “verdad”, porque sus teoremas se derivan de la lógica pura. Sin embargo, al mismo tiempo estos teoremas son extremadamente extraños y contradictorios. Incluso si usted tiene una capacidad limitada para trabajar con matemática (como es el caso de este servidor) sin duda se sorprenderá de algunos de los fenómenos que se indican a continuación:
5. Patrones (no tan) aleatorios.
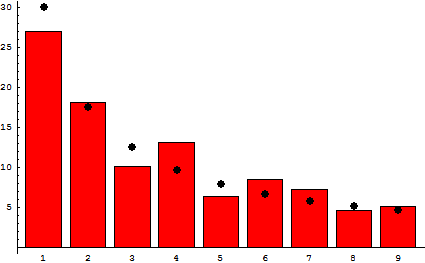
Curiosamente, incluso existen ciertos patrones en las listas aleatorias de datos (como el precio de las acciones en los mercados bursátiles y el número de habitantes de una ciudad): aproximadamente el 30% de los números comienza con el dígito 1, un porcentaje menor se iniciará con el dígito 2, otro inferior con el tercero, y así sucesivamente hasta que sólo uno de cada 20 números comiencen con 9. Cuanto mayor sea la lista de números, este patrón es más evidente.
4. Espirales de los números primos.
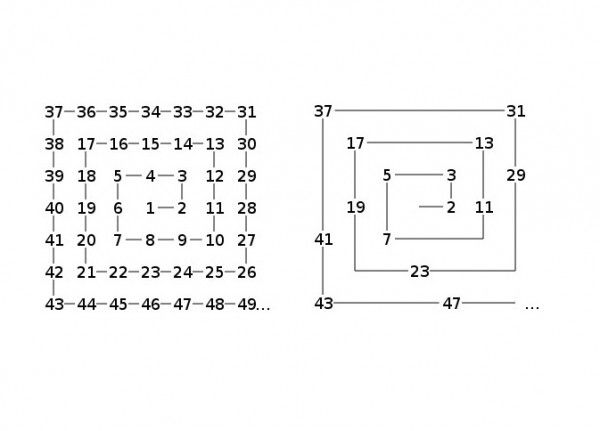
A primera vista, los números primos (los que sólo se puede dividir por 1 y ellos mismos) son distribuidos sin ningún orden entre los números enteros. Sin embargo, en 1963, mientras garabateaba en su libreta, el matemático Stanislaw Ulam se dio cuenta de que si los enteros están dispuestos en espiral, los números primos siempre caen en las líneas diagonales. Este patrón no es de por sí sorprendente (todos los primos excepto el 2 son impares, y las espirales se alternan entre pares e impares), pero un detalle genera curiosidad: tienden a agruparse en ciertas diagonales más que en otras independientemente de la cantidad que se ponga en el comienzo de la espiral, hay teorías que tratan de explicar el hecho, pero ninguna ha sido confirmada.
3. Inversión esférica.
https://www.youtube.com/watch?v=R_w4HYXuo9M
En la rama matemática de la topología, dos objetos se consideran equivalentes (homomórficos) si pueden ser transformadas entre sí sólo por estiramiento y torsión de sus superficies, si para hacer esto, es necesario doblar o cortar las superficies, se consideran diferentes.
Atentos a los misterios de su área de especialización, muchos matemáticos se preguntaran: ¿una esfera en su versión inversa sería homomórfica? En primer lugar, puede parecer que no, ya que sería necesario perforar la superficie de empuje y empujar la parte interna a través del agujero. Contrariando la idea inicial, el topólogo Bernard Morin ha encontrado una manera de voltear una esfera (no material, por supuesto) de adentro hacia afuera respetando las reglas de los objetos “iguales”. Más sorprendente que eso es el hecho de que Morin es ciego, lo que dificultó bastante el desarrollo de la técnica (ver en el vídeo de arriba).
2. Matemáticas de paredes.
A pesar de ser muchos, existe un número finito (matemáticamente hablando) de patrones geométricos posibles. Todos los dibujos de dos dimensiones del artista gráfico Maurits Cornelis Escher (1898 – 1972) encajan en uno de ellos (los llamados “grupos de papel tapiz”, que son 17 en total).
1. Soneto matemático.
“Al igual que un soneto de Shakespeare que captura la esencia misma del amor, o una pintura que trae la belleza de la forma humana y que va mucho más allá de la superficie, la ecuación de Euler llega a las profundidades de la existencia“, escribió el matemático Keith Devlin en su artículo “La ecuación más bella“, publicado en 2002. De manera terriblemente simple, la ecuación consigue unir tres conceptos matemáticos complejos.
La letra “e” representa un número irracional (con dígitos infinitos) que comienza con 2.71828. Descubierto en un estudio sobre el fenómeno de “intereses sobre intereses”, la “e” aparece en las secuencias que crecen exponencialmente, como una población de insectos o la tasa de desintegración de un elemento radioactivo.
Dado que la letra “i” representa un número imaginario: la raíz cuadrada de -1. Como su nombre lo indica, este número desafía las reglas de la realidad, porque hay un número que multiplicado por sí mismo da como resultado un número negativo, este extraño número es ampliamente utilizado en las ecuaciones matemáticas y fórmulas complejas.
Finalmente, el pi (π) es una constante que representa el resultado de dividir una circunferencia por su diámetro y también se utiliza en numerosas formulas matemáticas (más que los anteriores).
En la ecuación de Euler: “e” elevado a “i x pi” es igual a -1, y por lo tanto si se añade 1, es cero. Eso sí, no me pidas que te explique cómo utilizar esta ecuación, porque eso sería abusar de mis habilidades matemáticas.
Fuente: lifeslittlemysteries.com/2077-5-mind-boggling-math-facts.html


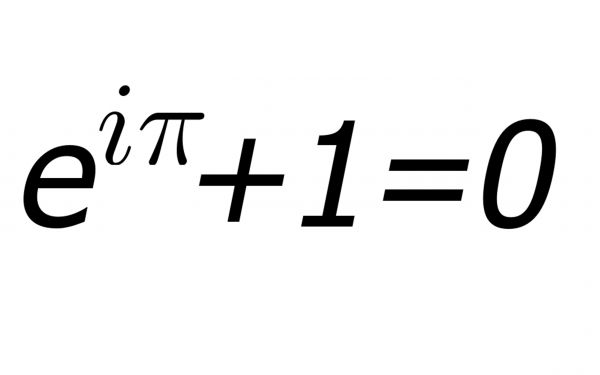
¡Excelente información! Felicidades.
Aquí está la ecuación en Wolfam Alpha:
La del soneto es fácil de demostrar, según la ecuación de Euler, e^(i*pi) = cos(pi) + isen(pi), el coseno es la parte real y el seno la imaginaria así que, si lo hacen en su calculadora (con los grados en radianes) tendrán que e^(i*pi) = -1 + i0, y si le suman 1, pues entonces tienen que e^(i*pi)+ 1 = 0. (Por cierto, pi equivale a 180°, así que pueden buscar incluso una gráfica en google del seno y coseno y verán que en ese punto, el coseno vale -1 y el seno vale 0).
Más claro no se puede.
Pi Rad = 180°
Me gusto mucho el de los números primos y después de leer veo que hay muchos tipos de patrones, en espiral, exagonal etc… el numero 5 lo investigue cuando fueron las elecciones de México, ya que según lo que dijeron varios académicos contradecía el resultado de las elecciones…
o.O?
ni uta idea del soneto =/
mi profe de topologia siempre decia q para la clase se debia asistir colocado “con harto material del bueno” para poder entenderla.
muy interesante dato
PPPF! AL MENOS NO SOY LA ÚNICA xD…
SALUDOS MARCIANOS
MADRES,DEBÍ HABER IDO A LA ESCUELA
No entendí un carajo…